
An Empirical Comparison of Supervised Learning Algorithms
Rich Caruana [email protected]
Alexandru Niculescu-Mizil [email protected]
Department of Computer Science, Cornell University, Ithaca, NY 14853 USA
Abstract
A number of supervised learning methods
have been introduced in the last decade. Un-
fortunately, the last comprehensive empiri-
cal evaluation of supervised learning was the
Statlog Project in the early 90’s. We present
a large-scale empirical comparison between
ten supervised learning methods: SVMs,
neural nets, logistic regression, naive bayes,
memory-based learning, random forests, de-
cision trees, bagged trees, boosted trees, and
boosted stumps. We also examine the effect
that calibrating the models via Platt Scaling
and Isotonic Regression has on their perfor-
mance. An important aspect of our study is
the use of a variety of performance criteria to
evaluate the learning methods.
1. Introduction
There are few comprehensive empirical studies com-
paring learning algorithms. STATLOG is perhaps the
best known study (King et al., 1995). STATLOG was
very comprehensive when it was performed, but since
then new learning algorithms have emerged (e.g., bag-
ging, boosting, SVMs, random forests) that have excel-
lent performance. An extensive empirical evaluation of
modern learning methods would be useful.
Learning algorithms are now used in many domains,
and different performance metrics are appropriate for
each domain. For example Precision/Recall measures
are used in information retrieval; medicine prefers
ROC area; Lift is appropriate for some marketing
tasks, etc. The different performance metrics measure
different tradeoffs in the predictions made by a clas-
sifier, and it is possible for learning methods to per-
form well on one metric, but be suboptimal on other
metrics. Because of this it is important to evaluate
algorithms on a broad set of performance metrics.
Appearing in Proceedings of the 23
rd
International Con-
ference on Machine Learning, Pittsburgh, PA, 2006. Copy-
right 2006 by the author(s)/owner(s).
This paper presents results of a large-scale empirical
comparison of ten supervised learning algorithms us-
ing eight performance criteria. We evaluate the perfor-
mance of SVMs, neural nets, logistic regression, naive
bayes, memory-based learning, random forests, deci-
sion trees, bagged trees, boosted trees, and boosted
stumps on eleven binary classification problems using
a variety of performance metrics: accuracy, F-score,
Lift, ROC Area, average precision, precision/recall
break-even point, squared error, and cross-entropy.
For each algorithm we examine common variations,
and thoroughly explore the space of parameters. For
example, we compare ten decision tree styles, neural
nets of many sizes, SVMs with many kernels, etc.
Because some of the performance metrics we examine
interpret model predictions as probabilities and mod-
els such as SVMs are not designed to predict probabil-
ities, we compare the performance of each algorithm
both before and after calibrating its predictions with
Platt Scaling and Isotonic Regression.
The empirical results are surprising. To preview: prior
to calibration, bagged trees, random forests, and neu-
ral nets give the best average performance across all
eight metrics and eleven test problems. Boosted trees,
however, are best if we restrict attention to the six
metrics that do not require probabilities. After cal-
ibration with Platt’s Method, boosted trees predict
better probabilities than all other methods and move
into first place overall. Neural nets, on the other hand,
are so well calibrated to begin with that they are hurt
slightly by calibration. After calibration with Platt’s
Method or Isotonic Regression, SVMs perform compa-
rably to neural nets and nearly as well as boosted trees,
random forests and bagged trees. Boosting full deci-
sion trees dramatically outperforms boosting weaker
stumps on most problems. On average, memory-based
learning, boosted stumps, single decision trees, logistic
regression, and naive bayes are not competitive with
the best methods. These generalizations, however, do
not always hold. For example, boosted stumps and
logistic regression, which perform poorly on average,
are the best models for some metrics on two of the test
problems.

An Empirical Comparison of Supervised Learning Algorithms
2. Methodology
2.1. Learning Algorithms
We attempt to explore the space of parameters and
common variations for each learning algorithm as thor-
oughly as is computationally feasible. This section
summarizes the parameters used for each learning al-
gorithm, and may safely be skipped by readers who
are easily bored.
SVMs: we use the following kernels in SVMLight
(Joachims, 1999): linear, polynomial degree 2 & 3, ra-
dial with width {0.001,0.005,0.01,0.05,0.1,0.5,1,2}. We
also vary the regularization parameter by factors of ten
from 10
−7
to 10
3
with each kernel.
ANN we train neural nets with gradient descent
backprop and vary the number of hidden units
{1,2,4,8,32,128} and the momentum {0,0.2,0.5,0.9}.
We halt training the nets at many different epochs
and use validation sets to select the best nets.
Logistic Regression (LOGREG): we train both
unregularized and regularized models, varying the
ridge (regularization) parameter by factors of 10 from
10
−8
to 10
4
.
Naive Bayes (NB): we use Weka (Witten & Frank,
2005) and try all three of the Weka options for han-
dling continuous attributes: modeling them as a single
normal, modeling them with kernel estimation, or dis-
cretizing them using supervised discretization.
KNN: we use 26 values of K ranging from K = 1 to
K = |trainset|. We use KNN with Euclidean distance
and Euclidean distance weighted by gain ratio. We
also use distance weighted KNN, and locally weighted
averaging. The kernel widths for locally weighted aver-
aging vary from 2
0
to 2
10
times the minimum distance
between any two points in the train set.
Random Forests (RF): we tried both the Breiman-
Cutler and Weka implementations; Breiman-Cutler
yielded better results so we report those here. The
forests have 1024 trees. The size of the feature set
considered at each split is 1,2,4,6,8,12,16 or 20.
Decision trees (DT): we vary the splitting crite-
rion, pruning options, and smoothing (Laplacian or
Bayesian smoothing). We use all of the tree models
in Buntine’s IND package (Buntine & Caruana, 1991):
BAYES, ID3, CART, CART0, C4, MML, and SMML.
We also generate trees of type C44LS (C4 with no
pruning and Laplacian smoothing), C44BS (C44 with
Bayesian smoothing), and MMLLS (MML with Lapla-
cian smoothing). See (Provost & Domingos, 2003) for
a description of C44LS.
Bagged trees (BAG-DT): we bag 100 trees of
each type described above. With boosted trees
(BST-DT) we boost each tree type as well. Boost-
ing can overfit, so we consider boosted trees af-
ter 2,4,8,16,32,64,128,256,512,1024 and 2048 steps
of boosting. With boosted stumps (BST-
STMP) we boost single level decision trees gener-
ated with 5 different splitting criteria, each boosted for
2,4,8,16,32,64,128,256,512,1024,2048,4096,8192 steps.
With LOGREG, ANN, SVM and KNN we scale at-
tributes to 0 mean 1 std. With DT, RF, NB, BAG-
DT, BST-DT and BST-STMP we don’t scale the data.
In total, we train about 2000 different models in each
trial on each problem.
2.2. Performance Metrics
We divide the eight performance metrics into three
groups: threshold metrics, ordering/rank metrics and
probability metrics.
The threshold metrics are accuracy (ACC), F-score
(FSC) and lift (LFT). See (Giudici, 2003) for a de-
scription of Lift Curves. Usually ACC and FSC have
a fixed threshold (we use 0.5). For lift, often a fixed
percent, p, of cases are predicted as positive and the
rest as negative (we use p = 25%). For thresholded
metrics, it is not important how close a prediction is
to a threshold, only if it is above or below threshold.
The ordering/rank metrics depend only on the order-
ing of the cases, not the actual predicted values. As
long as ordering is preserved, it makes no difference if
predicted values fall between 0 and 1 or 0.89 and 0.90.
These metrics measure how well the positive cases are
ordered before negative cases and can be viewed as
a summary of model performance across all possible
thresholds. The rank metrics we use are area under
the ROC curve (ROC), average precision (APR), and
precision/recall break even point (BEP). See (Provost
& Fawcett, 1997) for a discussion of ROC from a ma-
chine learning perspective.
The probability metrics, squared error (RMS) and
cross-entropy (MXE), interpret the predicted value of
each case as the conditional probability of that case
being in the positive class. See (Caruana & Niculescu-
Mizil, 2004) for a more detailed description of the eight
performance metrics.
2.3. Comparing Across Performance Metrics
Performance metrics such as accuracy or squared er-
ror have range [0, 1], while others (lift, cross entropy)
range from 0 to p where p depends on the data set.
For some metrics lower values indicate better perfor-

An Empirical Comparison of Supervised Learning Algorithms
mance. For others higher values are better. Metrics
such as ROC area have baseline rates that are indepen-
dent of the data, while others such as accuracy have
baseline rates that depend on the data. If baseline ac-
curacy is 0.98, an accuracy of 0.981 probably is not
good performance, but on another problem the Bayes
optimal rate might be 0.60 and achieving an accuracy
of 0.59 might be excellent performance.
To permit averaging across metrics and problems, per-
formances must be placed on comparable scales. We
do this by scaling performance for each problem and
metric from 0 to 1, where 0 is baseline performance
and 1 is Bayes optimal. Since the Bayes optimal rate
cannot be estimated on real problems, we use the best
observed performance as a proxy. The following base-
line model is used: predict p for every case, where p
is the percent of positives in the data.
1
Performances
are normalized to [0, 1], where 0 is baseline and 1 rep-
resents best performance. If a model performs worse
than baseline, its normalized score will be negative.
One disadvantage of normalized scores is that recov-
ering raw performances requires knowing the perfor-
mances at the top and bottom of the scale, and as new
best models are found the top of the scale may change.
The performances that define the top and bottom of
the scales for each problem and metric are available at
www.cs.cornell.edu\~caruana to allow comparison
with our results.
2.4. Calibration Methods
Some of the learning algorithms we examine are not
designed to predict probabilities. For example the out-
puts of an SVM are normalized distances to the deci-
sion boundary. And naive bayes models are known to
predict poorly calibrated probabilities because of the
unrealistic independence assumption.
A number of methods have been proposed for map-
ping predictions to posterior probabilities. Platt
(1999) proposed transforming SVM predictions to pos-
terior probabilities by passing them through a sigmoid.
Platt’s method also works well for boosted trees and
boosted stumps (Niculescu-Mizil & Caruana, 2005). A
sigmoid, however, might not be the correct transfor-
mation for all learning algorithms.
Zadrozny and Elkan (2002; 2001) used a more gen-
eral calibration method based on Isotonic Regression
(Robertson et al., 1988) to calibrate predictions from
SVMs, naive bayes, boosted naive bayes, and decision
trees. Isotonic Regression is more general in that the
1
For F-Score, baseline is calculated by predicting 1 for
all cases since predicting p can yield 0 F-Score.
Table 1. Description of problems
problem #attr train size test size %poz
adult 14/104 5000 35222 25%
bact 11/170 5000 34262 69%
cod 15/60 5000 14000 50%
calhous 9 5000 14640 52%
cov type 54 5000 25000 36%
hs 200 5000 4366 24%
letter.p1 16 5000 14000 3%
letter.p2 16 5000 14000 53%
medis 63 5000 8199 11%
mg 124 5000 12807 17%
slac 59 5000 25000 50%
only restriction it makes is that the mapping function
be isotonic (monotonically increasing). A standard al-
gorithm for Isotonic Regression that finds a piecewise
constant solution in linear time, is the pair-adjacent
violators (PAV) algorithm (Ayer et al., 1955).
To calibrate models, we use the same 1000 points val-
idation set that will be used for model selection.
2.5. Data Sets
We compare the algorithms on 11 binary classifica-
tion problems. ADULT, COV TYPE and LETTER
are from the UCI Repository (Blake & Merz, 1998).
COV TYPE has been converted to a binary problem
by treating the largest class as the positive and the
rest as negative. We converted LETTER to boolean in
two ways. LETTER.p1 treats ”O” as positive and the
remaining 25 letters as negative, yielding a very unbal-
anced problem. LETTER.p2 uses letters A-M as posi-
tives and the rest as negatives, yielding a well balanced
problem. HS is the IndianPine92 data set (Gualtieri
et al., 1999) where the difficult class Soybean-mintill is
the positive class. SLAC is a problem from the Stan-
ford Linear Accelerator. MEDIS and MG are medical
data sets. COD, BACT, and CALHOUS are three of
the datasets used in (Perlich et al., 2003). ADULT,
COD, and BACT contain nominal attributes. For
ANNs, SVMs, KNNs, and LOGREG we transform
nominal attributes to boolean (one boolean per value).
Each DT, BAG-DT, BST-DT, BST-STMP, RF, and
NB model is trained twice, once with transformed at-
tributes and once with the original ones. See Table 1
for characteristics of these problems.
3. Performances by Metric
For each test problem we randomly select 5000 cases
for training and use the rest of the cases as a large
final test set. We use 5-fold cross validation on the
An Empirical Comparison of Supervised Learning Algorithms
5000 cases to obtain five trials. For each trial we use
4000 cases to train the different models, 1000 cases to
calibrate the models and select the best parameters,
and then report performance on the large final test
set. We would like to run more trials, but this is a
very expensive set of experiments. Fortunately, even
with only five trials we are able to discern interesting
differences between methods.
Table 2 shows the normalized score for each algorithm
on each of the eight metrics. For each problem and
metric we find the best parameter settings for each al-
gorithm using the 1k validation sets set aside by cross-
validation, then report that model’s normalized score
on the final test set. Each entry in the table averages
these scores across the five trials and eight test prob-
lems. The second column tells if model predictions
were calibrated. A “–” means the model predictions
were not calibrated – they are the raw model predic-
tions. (The one exception is SVMs, where distances to
the separating hyperplane are linearly scaled to [0,1]
before computing the three probability metrics.) A
“PLT” or “ISO” in the second column indicates that
the model predictions were scaled after the model was
trained using Platt Scaling or Isotonic Regression, re-
spectively. These scaling methods were discussed in
Section 2.4. In the table, higher scores always indicate
better performance.
The second to last column, MEAN, is the mean nor-
malized score over the eight metrics, eleven problems,
and five trials. The models in the table are sorted by
the mean normalized score in this column. For now,
ignore the last column, OPT-SEL. This column will
be discussed later in this section.
In the table, the algorithm with the best performance
on each metric is boldfaced. Other algorithm’s whose
performance is not statistically distinguishable from
the best algorithm at p = 0.05 using paired t-tests on
the 5 trials are *’ed.
2
Entries in the table that are
neither bold nor starred indicate performance that is
significantly lower than the best models at p = 0.05.
3
2
Performing this many independent t-tests, each at
p = 0.05, is problematic. Some differences that are labeled
significant in the table probably are not truly significant
at p = 0.05. We considered applying a more stringent
experiment-wise p-value that takes into account the num-
ber of tests performed, but the strong correlations between
performances on different metrics, and on calibrated and
uncalibrated models, makes this problematic as well, so we
decided to keep it simple. Most of the differences in the ta-
ble are significant well beyond p = 0.05. Doing the t-tests
at p = 0.01 adds few additional stars to the table.
3
Note that it is possible for the difference between the
scores 0.90 and 0.89 to be statistically significant, and yet
for the same 0.90 score to be statistically indistinguishable
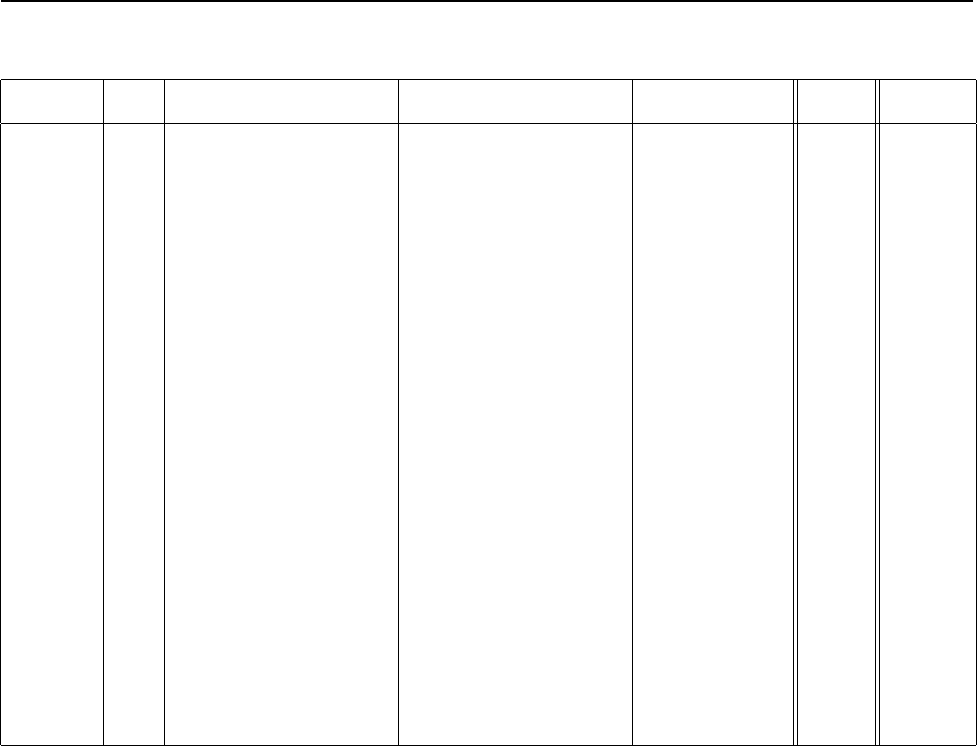
Averaging across all eight metrics, the strongest mod-
els are calibrated boosted trees, calibrated random
forests, bagged trees, PLT-calibrated SVMs and neu-
ral nets. If not calibrated, the best models overall are
bagged trees, random forests, and neural nets. With
or without calibration, the poorest performing models
are naive bayes, logistic regression, and decision trees.
Memory-based methods (e.g. KNN) are remarkably
unaffected by calibration, but exhibit mediocre overall
performance. Boosted stumps, even after calibration,
also have mediocre performance, and do not perform
nearly as well as boosted full trees.
Looking at individual metrics, boosted trees, which
have poor squared error and cross-entropy prior to cal-
ibration, dominate the other algorithms on these met-
rics after calibration. Bagged trees, random forests
and neural nets also predict good probabilities. Inter-
estingly, calibrating neural nets with PLT or ISO hurts
their calibration. If neural nets are trained well to be-
gin with it is better not to adjust their predictions.
Boosted trees also have excellent performance on or-
dering metrics: area under the ROC, average precision,
and the precision/recall break-even point.
4
Random
forests and bagged trees have similar performance as
boosted trees on these metrics. The neural nets and
SVMs also order cases extremely well.
On metrics that compare predictions to a thresh-
old: accuracy, F-score, and Lift, the best models are
calibrated or uncalibrated random forests, calibrated
boosted trees, and bagged trees with or without cali-
bration. We are not sure why ISO-calibration signifi-
cantly improves the F-Score of all models except NB,
including well-calibrated models such as neural nets
and bagged trees.
The last column, OPT-SEL, is the mean normalized
score for the eight metrics when model selection is done
by cheating and looking at the final test sets. The
means in this column represent the best performance
that could be achieved with each learning method if
model selection were done optimally. We present these
numbers because parameter optimization is more crit-
ical (and more difficult) with some algorithms than
with others. For example, bagging works well with
most decision tree types and requires little tuning, but
neural nets and SVMs require careful parameter selec-
tion. As expected, the mean normalized scores in the
from a poorer score of 0.88 if the variance of the 0.88 score
is higher than the variance of the 0.89 score.
4
PLT calibration does not change the ordering predicted
by models, so it does not affect these metrics. ISO calibra-
tion, however, can introduce ties in the predicted values
that may affect performance on the ordering metrics.
An Empirical Comparison of Supervised Learning Algorithms
Table 2. Normalized scores for each learning algorithm by metric (average over eleven problems)
model cal acc fsc lft roc apr bep rms mxe mean opt-sel
bst-dt plt .843* .779 .939 .963 .938 .929* .880 .896 .896 .917
rf plt .872* .805 .934* .957 .931 .930 .851 .858 .892 .898
bag-dt – .846 .781 .938* .962* .937* .918 .845 .872 .887* .899
bst-dt iso .826* .860* .929* .952 .921 .925* .854 .815 .885 .917*
rf – .872 .790 .934* .957 .931 .930 .829 .830 .884 .890
bag-dt plt .841 .774 .938* .962* .937* .918 .836 .852 .882 .895
rf iso .861* .861 .923 .946 .910 .925 .836 .776 .880 .895
bag-dt iso .826 .843* .933* .954 .921 .915 .832 .791 .877 .894
svm plt .824 .760 .895 .938 .898 .913 .831 .836 .862 .880
ann – .803 .762 .910 .936 .892 .899 .811 .821 .854 .885
svm iso .813 .836* .892 .925 .882 .911 .814 .744 .852 .882
ann plt .815 .748 .910 .936 .892 .899 .783 .785 .846 .875
ann iso .803 .836 .908 .924 .876 .891 .777 .718 .842 .884
bst-dt – .834* .816 .939 .963 .938 .929* .598 .605 .828 .851
knn plt .757 .707 .889 .918 .872 .872 .742 .764 .815 .837
knn – .756 .728 .889 .918 .872 .872 .729 .718 .810 .830
knn iso .755 .758 .882 .907 .854 .869 .738 .706 .809 .844
bst-stmp plt .724 .651 .876 .908 .853 .845 .716 .754 .791 .808
svm – .817 .804 .895 .938 .899 .913 .514 .467 .781 .810
bst-stmp iso .709 .744 .873 .899 .835 .840 .695 .646 .780 .810
bst-stmp – .741 .684 .876 .908 .853 .845 .394 .382 .710 .726
dt iso .648 .654 .818 .838 .756 .778 .590 .589 .709 .774
dt – .647 .639 .824 .843 .762 .777 .562 .607 .708 .763
dt plt .651 .618 .824 .843 .762 .777 .575 .594 .706 .761
lr – .636 .545 .823 .852 .743 .734 .620 .645 .700 .710
lr iso .627 .567 .818 .847 .735 .742 .608 .589 .692 .703
lr plt .630 .500 .823 .852 .743 .734 .593 .604 .685 .695
nb iso .579 .468 .779 .820 .727 .733 .572 .555 .654 .661
nb plt .576 .448 .780 .824 .738 .735 .537 .559 .650 .654
nb – .496 .562 .781 .825 .738 .735 .347 -.633 .481 .489
cheating column (OPT-SEL) tend to be higher than
the mean normalized scores when selection is done us-
ing 1k validation sets because model selection using
the validation sets does not always select the model
with the best performance on the final test set.
Comparing the MEAN and OPT-SEL columns, selec-
tion using 1k validation sets yields on average about
0.023 decrease in normalized score compared to op-
timal selection. As expected, high variance models
have the biggest drop in performance. Neural nets,
for example, which have relatively high variance, lose
substantial performance when selecting models with
1k validation sets, while other models such as random
forests, which have small variance, lose very little per-
formance when selection is done using 1k validation
sets. SVM’s have variance between RF and ANNs, and
thus lose more than RF, but less than ANN. Boosted
trees also have relatively high variance, but their over-
all performance after PLT or ISO calibration is so
strong that they remain the best model overall even
when selection is done using 1k validation sets.
4. Performances by Problem
Table 3 shows the normalized score for each algorithm
on each of the 11 test problems. Each entry is an
average over the eight performance metrics and five
trials when selection is done using 1k validation sets.
As the No Free Lunch Theorem suggests, there is no
universally best learning algorithm. Even the best
models (calibrated boosted trees, random forests and
bagged trees) perform poorly on some problems, and
models that have poor average performance perform
well on a few problems or metrics. For example, the
best models on ADULT are calibrated boosted stumps,
random forests and bagged trees. Boosted trees per-
form much worse. Bagged trees and random forests
also perform very well on MG and SLAC. On MEDIS,
the best models are random forests, neural nets and lo-
gistic regression. The only models that never exhibit
excellent performance on any problem are naive bayes
and memory-based learning.
Boosting full decision trees yields better performance

An Empirical Comparison of Supervised Learning Algorithms
Table 3. Normalized scores of each learning algorithm by problem (averaged over eight metrics)
model cal covt adult ltr.p1 ltr.p2 medis slac hs mg calhous cod bact mean
bst-dt plt .938 .857 .959 .976 .700 .869 .933 .855 .974 .915 .878* .896*
rf plt .876 .930 .897 .941 .810 .907* .884 .883 .937 .903* .847 .892
bag-dt – .878 .944* .883 .911 .762 .898* .856 .898 .948 .856 .926 .887*
bst-dt iso .922* .865 .901* .969 .692* .878 .927 .845 .965 .912* .861 .885*
rf – .876 .946* .883 .922 .785 .912* .871 .891* .941 .874 .824 .884
bag-dt plt .873 .931 .877 .920 .752 .885 .863 .884 .944 .865 .912* .882
rf iso .865 .934 .851 .935 .767* .920 .877 .876 .933 .897* .821 .880
bag-dt iso .867 .933 .840 .915 .749 .897 .856 .884 .940 .859 .907* .877
svm plt .765 .886 .936 .962 .733 .866 .913* .816 .897 .900* .807 .862
ann – .764 .884 .913 .901 .791* .881 .932* .859 .923 .667 .882 .854
svm iso .758 .882 .899 .954 .693* .878 .907 .827 .897 .900* .778 .852
ann plt .766 .872 .898 .894 .775 .871 .929* .846 .919 .665 .871 .846
ann iso .767 .882 .821 .891 .785* .895 .926* .841 .915 .672 .862 .842
bst-dt – .874 .842 .875 .913 .523 .807 .860 .785 .933 .835 .858 .828
knn plt .819 .785 .920 .937 .626 .777 .803 .844 .827 .774 .855 .815
knn – .807 .780 .912 .936 .598 .800 .801 .853 .827 .748 .852 .810
knn iso .814 .784 .879 .935 .633 .791 .794 .832 .824 .777 .833 .809
bst-stmp plt .644 .949 .767 .688 .723 .806 .800 .862 .923 .622 .915* .791
svm – .696 .819 .731 .860 .600 .859 .788 .776 .833 .864 .763 .781
bst-stmp iso .639 .941 .700 .681 .711 .807 .793 .862 .912 .632 .902* .780
bst-stmp – .605 .865 .540 .615 .624 .779 .683 .799 .817 .581 .906* .710
dt iso .671 .869 .729 .760 .424 .777 .622 .815 .832 .415 .884 .709
dt – .652 .872 .723 .763 .449 .769 .609 .829 .831 .389 .899* .708
dt plt .661 .863 .734 .756 .416 .779 .607 .822 .826 .407 .890* .706
lr – .625 .886 .195 .448 .777* .852 .675 .849 .838 .647 .905* .700
lr iso .616 .881 .229 .440 .763* .834 .659 .827 .833 .636 .889* .692
lr plt .610 .870 .185 .446 .738 .835 .667 .823 .832 .633 .895 .685
nb iso .574 .904 .674 .557 .709 .724 .205 .687 .758 .633 .770 .654
nb plt .572 .892 .648 .561 .694 .732 .213 .690 .755 .632 .756 .650
nb – .552 .843 .534 .556 .011 .714 -.654 .655 .759 .636 .688 .481
than boosting stumps only on seven problems. Occa-
sionally boosted stumps perform very well, but some-
times they perform very poorly so their average per-
formance is low. On ADULT, when boosting trees, the
first iteration of boosting hurts the performance of all
tree types, and never recovers in subsequent rounds.
When this happens even single decision trees outper-
form their boosted counterparts. Bagged trees and
random forests, however, consistently outperform sin-
gle trees on all problems. Bagging and random forests
are “safer” than boosting, even on the metrics for
which boosting yields the best overall performance.
5. Bootstrap Analysis
The results depend on the choice of problems and met-
rics. What impact might selecting other problems, or
evaluating performance on other metrics, have on the
results? For example, neural nets perform well on all
metrics on 10 of 11 problems, but perform poorly on
COD. If we hadn’t included the COD problem, neural
nets would move up 1-2 places in the rankings.
To help evaluate the impact of the choice of problems
and metrics we performed a bootstrap analysis. We
randomly select a bootstrap sample (sampling with
replacement) from the original 11 problems. For this
sample of problems we then randomly select a boot-
strap sample of 8 metrics from the original 8 metrics
(again sampling with replacement). For this bootstrap
sample of problems and metrics we rank the ten algo-
rithms by mean performance across the sampled prob-
lems and metrics (and the 5 folds). This bootstrap
sampling is repeated 1000 times, yielding 1000 poten-
tially different rankings of the learning methods.
Table 4 shows the frequency that each method ranks
1st, 2nd, 3rd, etc. The 0.228 entry for boosted trees
in the column for 2nd place, tells us that there is a
22.8% chance that boosted decision trees would have
placed 2nd in the table of results (instead of 1st) had
we selected other problems and/or metrics.
The bootstrap analysis complements the t-tests in Ta-
bles 2 and 3. The results suggest that if we had se-
lected other problems/metrics, there is a 58% chance
that boosted decision trees would still have ranked 1st

An Empirical Comparison of Supervised Learning Algorithms
Table 4. Bootstrap Analysis of Overall Rank by Mean Performance Across Problems and Metrics
model 1st 2nd 3rd 4th 5th 6th 7th 8th 9th 10th
bst-dt 0.580 0.228 0.160 0.023 0.009 0.000 0.000 0.000 0.000 0.000
rf 0.390 0.525 0.084 0.001 0.000 0.000 0.000 0.000 0.000 0.000
bag-dt 0.030 0.232 0.571 0.150 0.017 0.000 0.000 0.000 0.000 0.000
svm 0.000 0.008 0.148 0.574 0.240 0.029 0.001 0.000 0.000 0.000
ann 0.000 0.007 0.035 0.230 0.606 0.122 0.000 0.000 0.000 0.000
knn 0.000 0.000 0.000 0.009 0.114 0.592 0.245 0.038 0.002 0.000
bst-stmp 0.000 0.000 0.002 0.013 0.014 0.257 0.710 0.004 0.000 0.000
dt 0.000 0.000 0.000 0.000 0.000 0.000 0.004 0.616 0.291 0.089
logreg 0.000 0.000 0.000 0.000 0.000 0.000 0.040 0.312 0.423 0.225
nb 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.030 0.284 0.686
overall, and only a 4.2% chance of seeing them rank
lower than 3rd place. Random forests would come in
1st place 39% of the time, 2nd place 53% of the time,
with little chance (0.1%) of ranking below third place.
There is less than a 20% chance that a method other
than boosted trees, random forests, and bagged trees
would rank in the top three, and no chance (0.0%)
that another method would rank 1st—it appears to be
a clean sweep for ensembles of trees. SVMs probably
would rank 4th, and neural nets probably would rank
5th, but there is a 1 in 3 chance that SVMs would rank
after neural nets. The bootstrap analysis clearly shows
that MBL, boosted 1-level stumps, plain decision trees,
logistic regression, and naive bayes are not competitive
on average with the top five models on these problems
and metrics when trained on 5k samples.
6. Related Work
STATLOG is perhaps the best known study (King
et al., 1995). STATLOG was a very comprehensive
study when it was performed, but since then important
new learning algorithms have been introduced such as
bagging, boosting, SVMs, and random forests. LeCun
et al. (1995) presents a study that compares several
learning algorithms (including SVMs) on a handwrit-
ing recognition problem using three performance crite-
ria: accuracy, rejection rate, and computational cost.
Cooper et al. (1997) present results from a study that
evaluates nearly a dozen learning methods on a real
medical data set using both accuracy and an ROC-like
metric. Lim et al. (2000) perform an empirical com-
parison of decision trees and other classification meth-
ods using accuracy as the main criterion. Bauer and
Kohavi (1999) present an impressive empirical analy-
sis of ensemble methods such as bagging and boosting.
Perlich et al. (2003) conducts an empirical comparison
between decision trees and logistic regression. Provost
and Domingos (2003) examine the issue of predicting
probabilities with decision trees, including smoothed
and bagged trees. Provost and Fawcett (1997) discuss
the importance of evaluating learning algorithms on
metrics other than accuracy such as ROC.
7. Conclusions
The field has made substantial progress in the last
decade. Learning methods such as boosting, random
forests, bagging, and SVMs achieve excellent perfor-
mance that would have been difficult to obtain just 15
years ago. Of the earlier learning methods, feedfor-
ward neural nets have the best performance and are
competitive with some of the newer methods, particu-
larly if models will not be calibrated after training.
Calibration with either Platt’s method or Isotonic Re-
gression is remarkably effective at obtaining excellent
performance on the probability metrics from learning
algorithms that performed well on the ordering met-
rics. Calibration dramatically improves the perfor-
mance of boosted trees, SVMs, boosted stumps, and
Naive Bayes, and provides a small, but noticeable im-
provement for random forests. Neural nets, bagged
trees, memory based methods, and logistic regression
are not significantly improved by calibration.
With excellent performance on all eight metrics, cali-
brated boosted trees were the best learning algorithm
overall. Random forests are close second, followed by
uncalibrated bagged trees, calibrated SVMs, and un-
calibrated neural nets. The models that performed
poorest were naive bayes, logistic regression, decision
trees, and boosted stumps. Although some methods
clearly perform better or worse than other methods
on average, there is significant variability across the
problems and metrics. Even the best models some-
times perform poorly, and models with poor average

An Empirical Comparison of Supervised Learning Algorithms
performance occasionally perform exceptionally well.
Acknowledgments
We thank F. Provost and C. Perlich for the BACT,
COD, and CALHOUS data, C. Young for the SLAC
data, A. Gualtieri for the HS data, and B. Zadrozny
and C. Elkan for the Isotonic Regression code. This
work was supported by NSF Award 0412930.
References
Ayer, M., Brunk, H., Ewing, G., Reid, W., & Silver-
man, E. (1955). An empirical distribution function
for sampling with incomplete information. Annals
of Mathematical Statistics, 5, 641–647.
Bauer, E., & Kohavi, R. (1999). An empirical com-
parison of voting classification algorithms: Bagging,
boosting, and variants. Machine Learning, 36.
Blake, C., & Merz, C. (1998). UCI repository of ma-
chine learning databases.
Breiman, L. (1996). Bagging predictors. Machine
Learning, 24, 123–140.
Breiman, L. (2001). Random forests. Machine Learn-
ing, 45, 5–32.
Buntine, W., & Caruana, R. (1991). Introduction
to ind and recursive partitioning (Technical Report
FIA-91-28). NASA Ames Research Center.
Caruana, R., & Niculescu-Mizil, A. (2004). Data min-
ing in metric space: An empirical analysis of sup-
pervised learning performance criteria. Knowledge
Discovery and Data Mining (KDD’04).
Cooper, G. F., Aliferis, C. F., Ambrosino, R., Aronis,
J., Buchanan, B. G., Caruana, R., Fine, M. J., Gly-
mour, C., Gordon, G., Hanusa, B. H., Janosky, J. E.,
Meek, C., Mitchell, T., Richardson, T., & Spirtes,
P. (1997). An evaluation of machine learning meth-
ods for predicting pneumonia mortality. Artificial
Intelligence in Medicine, 9.
Giudici, P. (2003). Applied data mining. New York:
John Wiley and Sons.
Gualtieri, A., Chettri, S. R., Cromp, R., & Johnson,
L. (1999). Support vector machine classifiers as ap-
plied to aviris data. Proc. Eighth JPL Airborne Geo-
science Workshop.
Joachims, T. (1999). Making large-scale svm learning
practical. Advances in Kernel Methods.
King, R., Feng, C., & Shutherland, A. (1995). Statlog:
comparison of classification algorithms on large real-
world problems. Applied Artificial Intelligence, 9.
LeCun, Y., Jackel, L. D., Bottou, L., Brunot, A.,
Cortes, C., Denker, J. S., Drucker, H., Guyon, I.,
Muller, U. A., Sackinger, E., Simard, P., & Vapnik,
V. (1995). Comparison of learning algorithms for
handwritten digit recognition. International Con-
ference on Artificial Neural Networks (pp. 53–60).
Paris: EC2 & Cie.
Lim, T.-S., Loh, W.-Y., & Shih, Y.-S. (2000). A
comparison of prediction accuracy, complexity, and
training time of thirty-three old and new classifica-
tion algorithms. Machine Learning, 40, 203–228.
Niculescu-Mizil, A., & Caruana, R. (2005). Predicting
good probabilities with supervised learning. Proc.
22nd International Conference on Machine Learn-
ing (ICML’05).
Perlich, C., Provost, F., & Simonoff, J. S. (2003). Tree
induction vs. logistic regression: a learning-curve
analysis. J. Mach. Learn. Res., 4, 211–255.
Platt, J. (1999). Probabilistic outputs for support vec-
tor machines and comparison to regularized likeli-
hood methods. Adv. in Large Margin Classifiers.
Provost, F., & Domingos, P. (2003). Tree induction
for probability-based rankings. Machine Learning.
Provost, F. J., & Fawcett, T. (1997). Analysis and
visualization of classifier performance: Comparison
under imprecise class and cost distributions. Knowl-
edge Discovery and Data Mining (pp. 43–48).
Robertson, T., Wright, F., & Dykstra, R. (1988). Or-
der restricted statistical inference. New York: John
Wiley and Sons.
Schapire, R. (2001). The boosting approach to ma-
chine learning: An overview. In MSRI Workshop
on Nonlinear Estimation and Classification.
Vapnik, V. (1998). Statistical learning theory. New
York: John Wiley and Sons.
Witten, I. H., & Frank, E. (2005). Data mining: Prac-
tical machine learning tools and techniques. San
Francisco: Morgan Kaufmann. Second edition.
Zadrozny, B., & Elkan, C. (2001). Obtaining cali-
brated probability estimates from decision trees and
naive bayesian classifiers. ICML.
Zadrozny, B., & Elkan, C. (2002). Transforming clas-
sifier scores into accurate multiclass probability es-
timates. KDD.
