The margin of error is a statistic expressing the amount of random

Page 1 of 6

ESTIMATIONS

9.1 Margins of error and estimates: The margin of error is a statistic expressing

the amount of random sampling error in a survey's results. The larger the margin of

error, the less confidence one should have that the poll's reported results are close

to the "true" figures; that is, the figures for the whole population. Margin of error

occurs whenever a population is incompletely sampled.

Margin of error is often used in non-survey contexts to indicate observational

error in reporting measured quantities. In astronomy, for example, the convention

is to report the margin of error as, for example, 4.2421(16) light-years (the distance

to Proxima Centauri), with the number in parentheses indicating the expected

range of values in the matching digits preceding; in this case, 4.2421(16) is

equivalent to 4.2421 ± 0.0016.

[1]

The latter notation, with the "±", is more

commonly seen in most other science and engineering fields.

Explanation[edit]

The margin of error is usually defined as the "radius" (or half the width) of

a confidence interval for a particular statistic from a survey. One example is the

percent of people who prefer product A versus product B. When a single, global

margin of error is reported for a survey, it refers to the maximum margin of error

for all reported percentages using the full sample from the survey. If the statistic is

a percentage, this maximum margin of error can be calculated as the radius of the

confidence interval for a reported percentage of 50%.

The margin of error has been described as an "absolute" quantity, equal to a

confidence interval radius for the statistic. For example, if the true value is 50

percentage points, and the statistic has a confidence interval radius of 5 percentage

points, then we say the margin of error is 5 percentage points. As another example,

if the true value is 50 people, and the statistic has a confidence interval radius of 5

people, then we might say the margin of error is 5 people.

In some cases, the margin of error is not expressed as an "absolute" quantity; rather

it is expressed as a "relative" quantity. For example, suppose the true value is 50

people, and the statistic has a confidence interval radius of 5 people. If we use the

"absolute" definition, the margin of error would be 5 people. If we use the

"relative" definition, then we express this absolute margin of error as a percent of

the true value. So in this case, the absolute margin of error is 5 people, but the

"percent relative" margin of error is 10% (because 5 people are ten percent of 50

people). Often, however, the distinction is not explicitly made, yet usually is

apparent from context.

Page 2 of 6

Like confidence intervals, the margin of error can be defined for any desired

confidence level, but usually a level of 90%, 95% or 99% is chosen (typically

95%). This level is the probabilitythat a margin of error around the reported

percentage would include the "true" percentage. Along with the confidence level,

the sample design for a survey, and in particular its sample size, determines the

magnitude of the margin of error. A larger sample size produces a smaller margin

of error, all else remaining equal.

If the exact confidence intervals are used, then the margin of error takes into

account both sampling error and non-sampling error. If an approximate confidence

interval is used (for example, by assuming the distribution is normal and then

modeling the confidence interval accordingly), then the margin of error may only

take random sampling error into account. It does not represent other potential

sources of error or bias such as a non-representative sample-design, poorly phrased

questions, people lying or refusing to respond, the exclusion of people who could

not be contacted, or miscounts and miscalculations.

Concept

An example from the 2004 U.S. presidential campaign will be used to illustrate

concepts throughout this article. According to an October 2, 2004 survey

by Newsweek, 47% of registered voters would vote for John Kerry/John Edwards if

the election were held on that day, 45% would vote for George W. Bush/Dick

Cheney, and 2% would vote for Ralph Nader/Peter Camejo. The size of the

sample was 1,013. Unless otherwise stated, the remainder of this article uses a 95%

level of confidence.

Basic concept

Polls basically involve taking a sample from a certain population. In the case of

the Newsweek poll, the population of interest is the population of people who will

vote. Because it is impractical to poll everyone who will vote, pollsters take

smaller samples that are intended to be representative, that is, a random sample of

the population. It is possible that pollsters sample 1,013 voters who happen to vote

for Bush when in fact the population is evenly split between Bush and Kerry, but

this is extremely unlikely (p = 2

−1013

≈ 1.1 × 10

−305

) given that the sample is

random.

Sampling theory provides methods for calculating the probability that the poll

results differ from reality by more than a certain amount, simply due to chance; for

instance, that the poll reports 47% for Kerry but his support is actually as high as

50%, or is really as low as 44%. This theory and some Bayesian assumptions

suggest that the "true" percentage will probably be fairly close to 47%. The more

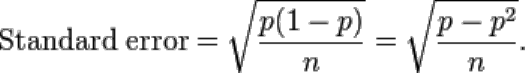
Page 3 of 6

people that are sampled, the more confident pollsters can be that the "true"

percentage is close to the observed percentage. The margin of error is a measure of

how close the results are likely to be.

However, the margin of error only accounts for random sampling error, so it is

blind to systematic errors that may be introduced by non-response or by

interactions between the survey and subjects' memory, motivation, communication

and knowledge.

Calculations assuming random sampling

This section will briefly discuss the standard error of a percentage,

the corresponding confidence interval, and connect these two concepts to the

margin of error. For simplicity, the calculations here assume the poll was based on

a simple random sample from a large population.

The standard error of a reported proportion or percentage p measures its accuracy,

and is the estimated standard deviation of that percentage. It can be estimated from

just p and the sample size, n, if n is small relative to the population size, using the

following formula:

When the sample is not a simple random sample from a large population, the

standard error and the confidence interval must be estimated through more

advanced calculations. Linearization and re-sampling are widely used techniques

for data from complex sample designs.

Note that there is not necessarily a strict connection between the true confidence

interval, and the true standard error. The true p percent confidence interval is the

interval [a, b] that contains p percent of the distribution, and where (100 − p)/2

percent of the distribution lies below a, and (100 − p)/2 percent of the distribution

lies above b. The true standard error of the statistic is the square root of the true

sampling variance of the statistic. These two may not be directly related, although

in general, for large distributions that look like normal curves, there is a direct

relationship.

In the Newsweek poll, Kerry's level of support p = 0.47 and n = 1,013. The

standard error (.016 or 1.6%) helps to give a sense of the accuracy of Kerry's

estimated percentage (47%). A Bayesian interpretation of the standard error is that

although we do not know the "true" percentage, it is highly likely to be located

within two standard errors of the estimated percentage (47%). The standard error

can be used to create a confidence interval within which the "true" percentage

should be to a certain level of confidence.

Page 4 of 6

The estimated percentage plus or minus its margin of error is a confidence interval

for the percentage. In other words, the margin of error is half the width of the

confidence interval. It can be calculated as a multiple of the standard error, with

the factor depending of the level of confidence desired; a margin of one standard

error gives a 68% confidence interval, while the estimate plus or minus 1.96

standard errors is a 95% confidence interval, and a 99% confidence interval runs

2.58 standard errors on either side of the estimate.

Definition

The margin of error for a particular statistic of interest is usually defined as the

radius (or half the width) of the confidence interval for that statistic. The term can

also be used to mean sampling error in general. In media reports of poll results, the

term usually refers to the maximum margin of error for any percentage from that

poll.

Different confidence levels

For a simple random sample from a large population, the maximum margin of

error is a simple re-expression of the sample size n. The numerators of these

equations are rounded to two decimal places.

Margin of error at 99% confidence

Margin of error at 95% confidence

Margin of error at 90% confidence

If an article about a poll does not report the margin of error, but does state that a

simple random sample of a certain size was used, the margin of error can be

calculated for a desired degree of confidence using one of the above formulae.

Also, if the 95% margin of error is given, one can find the 99% margin of error by

increasing the reported margin of error by about 30%.

As an example of the above, a random sample of size 400 will give a margin of

error, at a 95% confidence level, of 0.98/20 or 0.049 - just under 5%. A random

sample of size 1600 will give a margin of error of 0.98/40, or 0.0245 - just under

2.5%. A random sample of size 10 000 will give a margin of error at the 95%

confidence level of 0.98/100, or 0.0098 - just under 1%.

Maximum and specific margins of error

While the margin of error typically reported in the media is a poll-wide figure that

reflects the maximum sampling variation of any percentage based on all

respondents from that poll, the term margin of error also refers to the radius of the

confidence interval for a particular statistic.

Page 5 of 6

The margin of error for a particular individual percentage will usually be smaller

than the maximum margin of error quoted for the survey. This maximum only

applies when the observed percentage is 50%, and the margin of error shrinks as

the percentage approaches the extremes of 0% or 100%.

In other words, the maximum margin of error is the radius of a 95% confidence

interval for a reported percentage of 50%. If p moves away from 50%, the

confidence interval for p will be shorter. Thus, the maximum margin of error

represents an upper bound to the uncertainty; one is at least 95% certain that the

"true" percentage is within the maximum margin of error of a reported percentage

for any reported percentage.

Effect of population size

The formulae above for the margin of error assume that there is an infinitely

large population and thus do not depend on the size of the population of interest.

According to sampling theory, this assumption is reasonable when the sampling

fraction is small. The margin of error for a particular sampling method is

essentially the same regardless of whether the population of interest is the size of a

school, city, state, or country, as long as the sampling fraction is less than 5%.

In cases where the sampling fraction exceeds 5%, analysts can adjust the margin of

error using a "finite population correction", (FPC) to account for the added

precision gained by sampling close to a larger percentage of the population. FPC

can be calculated using the formula:

To adjust for a large sampling fraction, the fpc factored into the calculation of the

margin of error, which has the effect of narrowing the margin of error. It holds that

the fpc approaches zero as the sample size (n) approaches the population size (N),

which has the effect of eliminating the margin of error entirely. This makes

intuitive sense because when N = n, the sample becomes a census and sampling

error becomes moot.

Analysts should be mindful that the samples remain truly random as the sampling

fraction grows, lest sampling bias be introduced.

Other statistics

Confidence intervals can be calculated, and so can margins of error, for a range of

statistics including individual percentages, differences between percentages,

means, medians,

[9]

and totals.

Page 6 of 6

The margin of error for the difference between two percentages is larger than the

margins of error for each of these percentages, and may even be larger than the

maximum margin of error for any individual percentage from the survey.

Comparing percentages

In a plurality voting system, where the winner is the candidate with the most votes,

it is important to know who is ahead. The terms "statistical tie" and "statistical

dead heat" are sometimes used to describe reported percentages that differ by less

than a margin of error, but these terms can be misleading.

[10][11]

For one thing, the

margin of error as generally calculated is applicable to an individual

percentage and not the difference between percentages, so the difference between

two percentage estimates may not be statistically significant even when they differ

by more than the reported margin of error. The survey results also often provide

strong information even when there is not a statistically significant difference.

When comparing percentages, it can accordingly be useful to consider the

probability that one percentage is higher than another.

[12]

In simple situations, this

probability can be derived with 1) the standard error calculation introduced earlier,

2) the formula for the variance of the difference of two random variables, and 3) an

assumption that if anyone does not choose Kerry they will choose Bush, and vice

versa; they are perfectly negatively correlated. This may not be a tenable

assumption when there are more than two possible poll responses. For more

complex survey designs, different formulas for calculating the standard error of

difference must be used.

The standard error of the difference of percentages p for Kerry and q for Bush,

assuming that they are perfectly negatively correlated, follows:

Given the observed percentage difference p − q (2% or 0.02) and the standard error

of the difference calculated above (.03), any statistical calculator may be used to

calculate the probability that a sample from a normal distribution with mean 0.02

and standard deviation 0.03 is greater than 0.